UJI CHI KUADRAT

Rumus Chi Square

Chi Square disebut juga dengan Kai Kuadrat. Chi Square adalah salah satu jenis uji komparatif non parametris yang dilakukan pada dua variabel, di mana skala data kedua variabel adalah nominal. (Apabila dari 2 variabel, ada 1 variabel dengan skala nominal maka dilakukan uji chi square dengan merujuk bahwa harus digunakan uji pada derajat yang terendah). Berikut akan kita bahas tentang rumus chi square.

Syarat Uji Chi Square

Uji chi square merupakan uji non parametris yang paling banyak digunakan. Namun perlu diketahui syarat-syarat uji ini adalah: frekuensi responden atau sampel yang digunakan besar, sebab ada beberapa syarat di mana chi square dapat digunakan yaitu:

1. Tidak ada cell dengan nilai frekuensi kenyataan atau disebut juga Actual Count (F0) sebesar 0 (Nol).
2. Apabila bentuk tabel kontingensi 2 X 2, maka tidak boleh ada 1 cell saja yang memiliki frekuensi harapan atau disebut juga expected count (“Fh”) kurang dari 5.
3. Apabila bentuk tabel lebih dari 2 x 2, misak 2 x 3, maka jumlah cell dengan frekuensi harapan yang kurang dari 5 tidak boleh lebih dari 20%.

Jenis Uji Chi Square

Rumus chi-square sebenarnya tidak hanya ada satu. Apabila tabel kontingensi bentuk 2 x 2, maka rumus yang digunakan adalah “koreksi yates”. Untuk rumus koreksi yates, sudah kami bahas dalam artikel sebelumnya yang berjudul “Koreksi Yates“.

Apabila tabel kontingensi 2 x 2 seperti di atas, tetapi tidak memenuhi syarat seperti di atas, yaitu ada cell dengan frekuensi harapan kurang dari 5, maka rumus harus diganti dengan rumus “Fisher Exact Test”.

Pada artikel ini, akan fokus pada rumus untuk tabel kontingensi lebih dari 2 x 2, yaitu rumus yang digunakan adalah “Pearson Chi-Square”.

Rumus Pearson Chi Square

Rumus Chi Square Tersebut adalah:

Rumus Uji Chi Square

Untuk memahami apa itu “cell”, lihat tabel di bawah ini:

Tabel Kontingensi Chi Square

Tabel di atas, terdiri dari 6 cell, yaitu cell a, b, c, d, e dan f.

Sebagai contoh kita gunakan penelitian dengan judul “Perbedaan Pekerjaan Berdasarkan 

UJI  CHI  KUADRAT (c²) 

1. ​Pendahuluan

Uji Chi Kuadrat adalah pengujian hipotesis mengenai perbandingan antara : ​  ​​frekuensi observasi/yg benar-benar terjadi/aktual 

​dengan

​           ​frekuensi harapan/ekspektasi

1.1. ​Pengertian Frekuensi Observasi dan Frekuensi Harapan

​frekuensi observasi​ ​nilainya didapat dari hasil percobaan (o)​ 

  ​frekuensi harapan​​nilainya dapat dihitung secara teoritis (e)

Contoh :

1. ​Sebuah dadu setimbang dilempar sekali (1 kali) berapa nilai ekspektasi sisi-1, sisi-2, ​sisi-3, sisi-4, sisi-5 dan sisi-6 muncul?

kategori :	sisi-1	sisi-2	sisi-3	sisi-4	sisi-5	sisi-6
frekuensi ekspektasi (e)

2.​Sebuah dadu setimbang dilempar 120 kali berapa nilai ekspektasi sisi-1, sisi-2, ​sisi-3, sisi-4, sisi-5 dan sisi-6 muncul?

​

kategori :	sisi-1	sisi-2	sisi-3	sisi-4	sisi-5	sisi-6
frekuensi   ekspektasi (e)	20*)	20	20	20	20	20

​*) setiap  kategori memiliki frekuensi ekspektasi yang sama yaitu : x 120 = 20 

​Apakah data observasi akan sama dengan ekspektasi?

​Apakah jika anda melempar dadu 120 kali maka pasti setiap sisi akan muncul ​sebanyak 20 kali? 

​Coba lempar dadu sebanyak 120 kali, catat hasilnya, berapa frekuensi ​kemunculan setiap sisi? 

          Catatan saudara tersebut adalah frekuensi observasi.

1.2. ​Bentuk Distribusi Chi Kuadrat (c²)

Nilai c² adalah nilai kuadrat karena itu nilai c² selalu positif.

​

Bentuk distribusi c² tergantung dari derajat bebas(db)/degree of freedom.

Perhatikan Tabel hal 178 dan 179 (Buku Statistika-2, Gunadarma).

Anda bisa membacanya?

Contoh : ​Berapa nilai c² untuk  db =  5 dengan = 0.010?    (15.0863)

​Berapa nilai c² untuk  db =  17 dengan = 0.005?  (35.7185)

Pengertian pada Uji c² sama dengan pengujian hipotesis yang lain, yaitu luas daerah penolakan  atau taraf nyata pengujian 

Perhatikan gambar berikut :

​

​

​a : luas daerah penolakan  = taraf nyata pengujian

​

      0​          + ¥

1.3.​Pengunaan Uji  c²

Uji c²  dapat digunakan untuk :​

a.  ​Uji Kecocokan = Uji kebaikan-suai = Goodness of fit

​b. ​Uji Kebebasan 

c. ​Uji beberapa proporsi 

Prinsip pengerjaan (b) dan (c) sama saja

2.​Uji Kecocokan

2.1​Penetapan Hipotesis Awal dan Hipotesis Alternatif

:  frekuensi setiap kategori memenuhi suatu nilai/perbandingan. 

 : Ada kategori yang tidak memenuhi nilai/perbandingan tersebut.

Contoh 1 :

Pelemparan dadu 120 kali, kita akan menguji kesetimbangan dadu .  Dadu setimbang jika setiap sisi dadu akan muncul 20 kali.

​:​setiap sisi akan muncul = 20 kali. 

​:​ada sisi yang muncul 20 kali.

Contoh 2 :

Sebuah mesin pencampur adonan es krim akan menghasilkan perbandingan antara 

Coklat :  Gula :  Susu : Krim = 5 : 2 : 2 : 1

​:​perbandingan Coklat : Gula : Susu : Krim =  5 : 2 : 2 : 1

​:​perbandingan Coklat : Gula : Susu : Krim 5 : 2 : 2 : 1

2.2 ​Rumus  c²

​

​  k  :  banyaknya kategori/sel, 1,2 ... k

​   :  frekuensi observasi untuk kategori  ke-i

​   :  frekuensi ekspektasi untuk kategori ke-i  

        kaitkan dengan frekuensi ekspektasi dengan nilai/perbandingan dalam 

Derajat Bebas (db) = k - 1

​

2.3​Perhitungan c²

Contoh  3 :

Pelemparan dadu sebanyak 120 kali menghasilkan data sebagai berikut :

kategori :	sisi-1	sisi-2	sisi-3	sisi-4	sisi-5	sisi-6
frekuensi observasi	20 20	20 22	20 17	20 18	20 19	20 24

*) Nilai dalam kotak kecil adalah frekuensi ekspektasi

Apakah dadu itu dapat dikatakan setimbang?

Lakukan pengujian dengan taraf nyata = 5 %

Solusi ​:

1.​​:​Dadu setimbang semua sisi akan muncul = 20 kali.

​​:​Dadu tidak setimbang ada sisi yang muncul 20 kali.

2.​Statistik Uji c²

3.​Nilai = 5 % = 0.05

​k = 6 ; db = k - 1 = 6-1 = 5

4.​Nilai Tabel c²​

k = 6 ; db = k - 1 = 6-1 = 5

db = 5; = 0.05 c² tabel = 11.0705

5.​Wilayah Kritis​= Penolakan  jika  c² hitung  > c² tabel (db; a)

​           c² hitung > 11.0705

6. ​Perhitungan c²​

​

​ ​(catatan : Gunakan tabel seperti ini agar pengerjaan lebih sistematik)

​

kategori :			(-)	(-)²	(-)²/
sisi-1	20	20	0	0	0
sisi-2	22	20	2	4	0.20
sisi-3	17	20	-3	9	0.45
sisi-4	18	20	-2	4	0.20
sisi-5	19	20	-1	1	0.05
sisi-6	24	20	4	16	0.80
	120	120	---------	--------------	1.70

    c²  hitung = 1.70

7.​Kesimpulan :

​c²  hitung = 1.70 <  c² tabel 

​Nilai c²  hitung ada di daerah penerimaan 

​ diterima; pernyataan dadu setimbang dapat diterima.

Contoh 4 :

Sebuah mesin pencampur adonan es krim akan menghasilkan perbandingan antara Coklat :  Gula :  Susu : Krim = 5 : 2 : 2 : 1.  Jika 500 kg adonan yang dihasilkan,  diketahui mengandung 275 kg Coklat, 95 kg Gula, 70 kg Susu dan 60 kg Krim, apakah mesin itu bekerja sesuai  dengan perbandingan yang telah ditentukan?  Lakukan pengujian dengan taraf nyata = 1 %.

Solusi :

1.  ​:​perbandingan Coklat : Gula : Susu : Krim  =  5 : 2 : 2 : 1

    ​:​perbandingan Coklat : Gula : Susu : Krim   5 : 2 : 2 : 1

2.​Statistik Uji c²

3.​Nilai = 1 % = 0.01

4.​Nilai Tabel c²

k = 4;  db =k -1 = 4-1= 3

db = 3;​ = 0.01 c² tabel = 11.3449

5.​Wilayah Kritis​= Penolakan  jika  c² hitung  > c² tabel (db; a)

​          c² hitung  > 11.3449

6. ​Perhitungan c²

​

kategori :			(-)	(-)²	(-)²/
Coklat	275	250*)	25	625	2.50
Gula	95	100	-5	25	0.25
Susu	70	100	-30	900	9.00
Krim	60	50	10	100	2.00
S	500	500	-----------	--------	13.75

*)​Perbandingan Coklat : Gula : Susu : Krim = 5 : 2 : 2 :1

​Dari 500 kg adonan Nilai ekspektasi  Coklat = 5/10 x 500 = 250 kg

​Nilai ekspektasi  Gula =  2/10 x 500 = 100 kg

​Nilai ekspektasi  Susu = 2/10 x 500 = 100 kg

​Nilai ekspektasi  Krim =  1/10 x 500 =   50 kg

c² hitung = 13.75

7.​ Kesimpulan :

​c² hitung >  c² tabel ( 13.75 > 11.3449)

​ ditolak, ​ diterima.  

Perbandingan Coklat : Gula : Susu : Krim ¹ 5 : 2 : 2 :1 

3.​Uji Kebebasan dan Uji Beberapa Proporsi

Uji kebebasan antara 2 variabel memiliki prinsip pengerjaan yang sama dengan pengujian beberapa proporsi. 

(Berbeda hanya pada penetapan Hipotesis awal dan hipotesis alternatif)

3.1​Penetapan Hipotesis Awal dan Hipotesis Alternatif 

A.​Uji Kebebasan :

​ :  ​variabel-variabel saling bebas    ​

​ :​variabel-variabel tidak saling bebas​

B​Uji Beberapa Proporsi :

​:   ​setiap proporsi bernilai sama  ​

​:​ada  proporsi yang bernilai tidak sama​

3.2​Rumus Uji 

Data dalam pengujian ketergantungan dan beberapa proporsi disajikan dalam bentuk Tabel Kontingensi.

Bentuk umum Tabel Kontingensi berukuran r baris x k kolom

                  

                 derajat bebas = (r-1)(k-1)

                 r : banyak baris

                 k : banyak kolom

                : frekuensi observasi baris ke-i, kolom ke-j 

                : frekuensi ekspektasi baris ke-i, kolom ke-j

3.3​Perhitungan c²

Contoh 5 : ​

​

Kita akan  menguji kebebasan antara faktor gender (jenis kelamin) dengan jam kerja di suatu pabrik.  Tabel kontingensi dapat dibuat sebagai berikut :

	pria	wanita	Total Baris
Kurang dari 25 jam/minggu	2.33   2	2.67 3	5
25 sampai 50 jam/minggu	6.07      7	6.93 6	13
lebih dari 50 jam/minggu	5.60 5	6.40 7	12
Total Kolom	14	16	Total Observasi=   30

*) ​Nilai dalam kotak kecil adalah frekuensi ekspektasi

Perhatikan cara mendapatkan frekuensi ekspektasi!

Apakah ada kaitan antara gender dengan jam kerja?  

Lakukan pengujian  kebebasan variabel dengan taraf uji 5 %

Ukuran Tabel Kontingensi  di atas = 3 x 2 ( 3 baris dan 2 kolom)

db = (3-1)(2-1) = 2 x 1 = 2

Solusi :

1.​​ :    Gender  dan Jam kerja saling bebas​

​​ :     Gender dan Jam kerja tidak saling bebas

2.​Statistik Uji = c²

3.​Nilai   = 5 % = 0.05

4.​Nilai Tabel c²  db = 2; = 0.05 c² tabel  = 5.99147

5.​Wilayah Kritis : Penolakan ​ c² hitung > c² tabel 

​    c² hitung > 5.99147

6.​Perhitungan c²​

    

frekuensi harapan untuk :​

pria, < 25 jam ​= ​    ​pria, 25-50 jam = ​

pria, > 50 jam   = ​

wanita, < 25 jam  = ​    ​wanita, 25-50 jam =​

​

wanita, > 50 jam = ​

Selesaikan Tabel perhitungan c²  di bawah ini.

​

kategori :			(-)	(-)²	(-)²/
P, < 25	2	2.33	-0.33	0.1089	0.1089/2.33 =  0.0467
P, 25 - 50	7	6.07	0.93	0.8649	0.1425
P, > 50	5	5.60	-0.60	0.36	0.0643
W, < 25	3	2.67	0.33	0.1089	0.0408
W, 25-50	6	6.93	-0.93	0.8649	0.1249
W, >50	7	6.40	0.60	0.36	0.0563
	------	-----	--------	---------	c² hitung =       0.4755

​

7.​Kesimpulan

​c² hitung < c² tabel (0.4755 < 5.99147)

​c² hitung ada di daerah penerimaan 

​ diterima, gender dan jam kerja saling bebas

Catatan : ​Kesimpulan hanya menyangkut kebebasan antar variabel dan bukan    

hubungan sebab-akibat (hubungan kausal)

Contoh 6 :

Berikut adalah data proporsi penyiaran film(satuan pengukuran dalam persentase (%) jam siaran TV) di 3 stasiun TV.  Apakah proporsi pemutaran Film India, Kungfu dan Latin di ketiga stasiun Tv tersebut sama?   Lakukan Pengujian proporsi dengan Taraf Nyata = 2.5 %

​	ATV (%)	BTV (%)	CTV (%)	Total Baris (%)
Film India	4.17 4.5	2.92 3.5	2.92 2.0	10
Film Kungfu	3.33 2.5	2.33       1.0	2.33 4.5	8
Film Latin	2.50     3.0	1.75 2.5	1.75 0.5	6
Total Kolom               (%)	10	7	7	Total Observasi (%) =               24

*) ​Nilai dalam kotak kecil adalah frekuensi ekspektasi

Perhatikan cara mendapatkan frekuensi ekspektasi!

Ukuran Tabel Kontingensi  di atas = 3 x 3( 3 baris dan 3 kolom)

db = (3-1)(3-1) = 2 x 2 =  4

Solusi :

1.​ :     Proporsi pemutaran film India, Kungfu dan Latin di ketiga stasiun 

TV adalah sama.

 :    Ada  proporsi pemutaran film India, Kunfu dan Latin di ketiga stasiun TV yang tidak sama.

  Pendidikan”.

Maka kita coba gunakan data sebagai berikut:

Contoh Tabulasi Untuk Uji Chi Square

Dari data di atas, kita kelompokkan ke dalam tabel kontingensi. Karena variabel pendidikan memiliki 3 kategori dan variabel pekerjaan memiliki 2 kategori, maka tabel kontingensi yang dipakai adalah tabel 3 x 2. Maka akan kita lihat hasilnya sebagai berikut:

Contoh Tabel Kontingensi Chi-Square

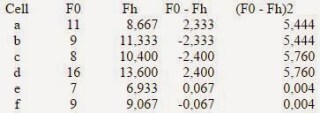
Membuat Frekuensi Kenyataan (F0) Rumus Chi Square

Dari tabel di atas, kita inventarisir per cell untuk mendapatkan nilai frekuensi kenyataan, sebagai berikut:

Membuat Frekuensi Kenyataan (F0) Rumus Chi Square

Langkah berikutnya kita hitung nilai frekuensi harapan per cell, rumus menghitung frekuensi harapan adalah sebagai berikut:

Fh= (Jumlah Baris/Jumlah Semua) x Jumlah Kolom

1. Fh cell a = (20/60) x 26 = 8,667
2. Fh cell b = (20/60) x 34 = 11,333
3. Fh cell c = (24/60) x 26 = 10,400
4. Fh cell d = (24/60) x 34 = 13,600
5. Fh cell e = (16/60) x 26 = 6,933
6. Fh cell f = (16/60) x 34 = 9,067

Maka kita masukkan ke dalam tabel sebagai berikut:

Hitung Fh Rumus Chi Square

Membuat Kuadrat Frekuensi Kenyataan Rumus Chi Square

Langkah berikutnya adalah menghitung Kuadrat dari Frekuensi Kenyataan dikurangi Frekuensi Harapan per cell.

1. Fh cell a = (11 – 8,667)2 = 5,444
2. Fh cell b = (9 – 11,333)2 = 5,444
3. Fh cell c = (8 – 10,400)2 = 5,760
4. Fh cell d = (16 – 13,600)2 = 5,760
5. Fh cell e = (7 – 6,933)2 = 0,004
6. Fh cell f = (9 – 9,067)2 = 0,004

Lihat hasilya pada tabel di bawah ini:

Tabel Hitung Chi- Square

Hitung Nilai Chi Square

Kuadrat dari Frekuensi Kenyataan dikurangi Frekuensi Harapan per cell kemudian dibagi frekuensi harapannya:

1. Fh cell a = 5,444/8,667 = 0,628
2. Fh cell b = 5,444/11,333 = 0,480
3. Fh cell c = 5,760/10,400 = 0,554
4. Fh cell d = 5,760/13,600 = 0,424
5. Fh cell e = 0,004/6,933 = 0,001
6. Fh cell f = 0,004/9,067 = 0,000

Kemudian dari nilai di atas, semua ditambahkan, maka itulah nilai chi-square hitung. Lihat Tabel di bawah ini:

Maka Nilai Chi-Square Hitung adalah sebesar: 2,087.

Chi Square Hitung VS Chi Square Tabel

Untuk menjawab hipotesis, bandingkan chi-square hitung dengan chi-square tabel pada derajat kebebasan atau degree of freedom (DF) tertentu dan taraf signifikansi tertentu. Apabila chi-square hitung >= chi-square tabel, maka perbedaan bersifat signifikan, artinya H0 ditolak atau H1 diterima.

DF pada contoh di atas adalah 2. Di dapat dari rumus -> DF = (r – 1) x (c-1)

di mana: r = baris. c = kolom.

Pada contoh di atas, baris ada 3 dan kolom ada 2, sehingga DF = (2 – 1) x (3 -1) = 2.

Apabila taraf signifikansi yang digunakan adalah 95% maka batas kritis 0,05 pada DF 2, nilai chi-square tabel sebesar = 5,991.

Karena 2,087 < 5,991 maka perbedaan tidak signifikan, artinya H0 diterima atau H1 ditolak.