NAMA           :    RIZKIANTO

NPM               :    17 630 028

NILAI SENTRAL

A.    Pengertan nilai sentral

Nilai sentral atau nilai rata-rata juga disebut nilai tengah dari sekumpulan data statistik adalah suatu nilai dalam kumpulan atau rangkaian data yang dapat mewakili kumpulan atau rangkaian data tersebut. Suatu rangkaian data biasanya memiliki tendensi(kecenderungan) untuk memusat pada nilai sentral ini. Dari sekumpulan data (distribusi), ada beberapa harga/nilai yang dapat kita anggap sebagai wakil dari kelompok data. Nilai-nilai yang biasa digunakan untuk mewakili data tersebut adalah mean dan modus disebut sebagai nilai tengah (central tendency).

Suatu nilai dapat disebut sebagai nilai sentral apabila memiliki persyaratan sebagai berikut:

1.      Nilai sentral harus dapat mewakili rangkaian data.

2.      Perhitungannya harus didasarkan pada seluruh data.

3.      Perhitungannya harus obyektif.

4.      Perhitungannya mudah.

5.      Dalam satu rangkaian data hanya ada satu nilai sentral.

B.     Jenis atau macam nilai sentral

1.      Rata -rata hitung ( mean )

Mean adalah nilai rata-rata dari beberapa buah data. Nilai mean dapat ditentukan dengan membagi jumlah data dengan banyaknya data. Mean (rata-rata) merupakan suatu ukuran pemusatan data. Mean suatu data juga merupakan statistik karena mampu menggambarkan bahwa data tersebut berada pada kisaran mean data tersebut.

a)      Rumus Mean Hitung dari Data Tunggal

b)      Rumus Mean Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi

 

2. Median

            Median menentukan letak tengah data setelah data disusun menurut urutan  nilainya. Bisa juga nilai tengah dari data-data yang terurut. Simbol untuk median adalah Me.  Dengan median Me, maka 50% dari banyak data nilainya paling tinggi sama dengan Me, dan 50% dari banyak data nilainya paling rendah sama dengan Me. Dalam  mencari median, dibedakan  untuk banyak data ganjil  dan banyak data genap.  Untuk  banyak data ganjil, setelah data disusun menurut nilainya, maka median Me adalah data yang terletak tepat di tengah. Median bisa dihitung menggunakan rumus sebagai berikut:

 

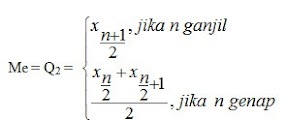
Contoh:

Dari lima kali kuiz statistika, seorang mahasiswa memperoleh nilai 82, 93, 86, 92, dan 79. Tentukan median populasi ini. jawab: Setelah data disusun dari yang terkecil sampai terbesar, diperoleh  79 82 86 92 93 Oleh karena itu medianya adalah 86
Kada nikotin yang berasal dari sebuah contoh acak enam batang rokok cap tertentu adalah 2.3, 2.7, 2.5, 2.9, 3.1, dan 1.9 miligram. Tentukan mediannya.

jawab:

Bila kadar nikotin itu diurutkan dari yang terkecil sampai terbesar, maka diperoleh 1.9 2.3 2.5 2.7 2.9 3.1 Maka mediannya adalah rata-rata dari 2.5 dan 2.7, yaitu 

 

Selain itu juga dapat dicari median dari data yang telah tersusun dalam bentuk distribusi frekuensi. Rumus yang digunakan ada dua, yaitu

 

Dimana :

Bak  = batas kelas atas median

c      =  lebar kelas

s’  = selisih antara nomor frekuensi median dengan frekuensi kumulatif sampai kelas   median

M    = frekuensi kelas median

Sebelum menggunakan kedua rumus di atas, terlebih dahulu harus ditentukan kelas yang menjadi kelas median. Kelas median adalah kelas yang memuat nomor frekuensi median, dan nomor frekuensi median ini ditentukan dengan membagi keseluruhan data dengan dua. Secara singkat rumus median dapat digunakan sebagai berikut dalam perhitungan menggunakan tabel data

 

Keterangan

Md : Nilai Median

L       : Tepi bawah dari kelas yang mengandung median

n       : Jumlah data

fc      : frekuensi komulatif pada kelas sebelum kelas median

fm     : frekuensi (absolut) darikelas terdapatnya median

C      : Kelas interval

3    3.   Modus

Modus adalah nilai yang sering muncul. Jika kita tertarik pada data frekuensi, jumlah dari suatu nilai dari kumpulan data, maka kita menggunakan modus. Modus sangat baik bila digunakan untuk data yang memiliki sekala kategorik yaitu nominal atau ordinal.
Sedangkan data ordinal adalah data kategorik yang bisa diurutkan, misalnya kita menanyakan kepada 100 orang tentang kebiasaan untuk mencuci kaki sebelum tidur, dengan pilihan jawaban: selalu (5), sering (4), kadang-kadang(3), jarang (2), tidak pernah (1). Apabila kita ingin melihat ukuran pemusatannya lebih baik menggunakan modus yaitu yaitu jawaban yang paling banyak dipilih, misalnya sering (2). Berarti sebagian besar orang dari 100 orang yang ditanyakan menjawab sering mencuci kaki sebelum tidur. Inilah cara menghitung modus:

§   Data yang belum dikelompokkan

Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo.

§  Data yang telah dikelompokka

Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:

Dengan :

Mo      =  Modus

L     =Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas
b1  =Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2      = frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sesudahnya

Contoh:

Sumbangan dari warga Bogor pada hari Palang Merah Nasional tercatat sebagai berikut: Rp 9.000, Rp 10.000, Rp 5.000, Rp 9.000, Rp 9.000, Rp 7.000, Rp 8.000, Rp 6.000, Rp 10.000, Rp 11.000. Maka modusnya, yaitu nilai yang terjadi dengan frekuensi paling tinggi, adalah Rp 9.000. Dari dua belas pelajar sekolah lanjutan tingkat atas yang diambil secara acak dicatat berapa kali mereka menonton film selama sebulan lalu. Data yang diperoleh adalah 2, 0, 3, 1, 2, 4, 2, 5, 4, 0, 1 dan 4. Dalam kasus ini terdapat dua modu, yaitu 2 dan 4, karena 2 dan 4 terdapat dengan frekuensi tertinggi. Distribusi demikian dikatakan bimodus.